Mastering Class Imbalance in Machine Learning - Part 1: Evaluating Model Performance
Introduction
In the world of machine learning, encountering imbalanced datasets is a common challenge. Class imbalance occurs when one class significantly outnumbers the other(s), leading to biased model performance.
In this two-part tutorial series, we will delve into the intricacies of the class imbalance problem and discuss effective strategies to address it.
In Part 1, we will focus on the importance of selecting appropriate evaluation metrics for imbalanced datasets and explore four essential metrics: Precision, Recall, F1 Score, and ROC Curve.
Understanding Class Imbalance
Before we dive into evaluation metrics, let's gain a clear understanding of class imbalance. In a binary classification problem, class imbalance occurs when one class (referred to as the minority class) has a considerably smaller number of instances compared to the other class (majority class). This imbalance can adversely affect model performance, as the model might become biased towards predicting the majority class, ignoring the minority class entirely.
The Pitfall of Accuracy
Traditional evaluation metrics like accuracy may not be suitable for imbalanced datasets. Accuracy measures the overall correct predictions, which can be misleading when one class heavily dominates the others. The formula for accuracy is given below,
\[Accuracy = \frac{\text{Number of Correct Predictions}}{\text{Total Number of Predictions}} \]
For instance, if the majority class accounts for 90% of the data, a model that predicts all instances as the majority class will still achieve 90% accuracy. This apparent high accuracy masks the model's inability to accurately classify the minority class.
Precision
Precision is a vital metric in imbalanced datasets that quantifies the accuracy of positive predictions made by the model. It calculates the ratio of true positive predictions to the total positive predictions (both true and false). High precision indicates that when the model predicts an instance as positive, it is likely to be correct. Precision is given by,
\[Precision = \frac{\text{True Positives}}{\text{True Positives + False Positives}} \]
Recall (Sensitivity or True Positive Rate)
Recall measures the model's ability to correctly identify positive instances from the entire actual positive class. In the context of class imbalance, recall is crucial as it highlights the model's capacity to find minority class samples. It is calculated as follows,
\[Recall = \frac{\text{True Positives}}{\text{True Positives + False Negatives}} \]
F1 Score
The F1 Score is the harmonic mean of precision and recall. It is a single metric that balances both precision and recall, providing a comprehensive evaluation of model performance on imbalanced datasets. F1 Score is ideal for situations where you need to strike a balance between precision and recall. It is computed as,
\[F1 Score = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision + Recall}} \]
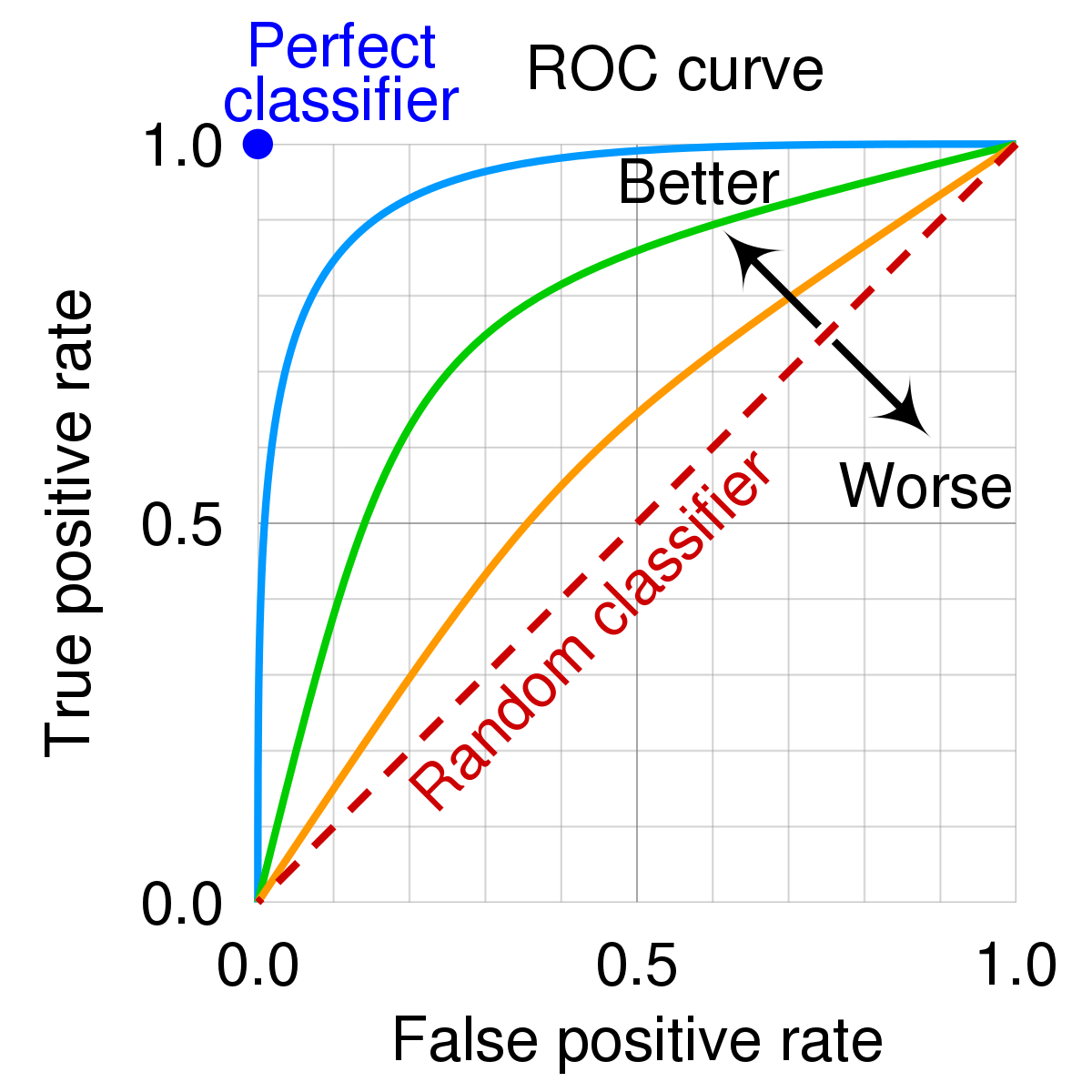
ROC Curve (Receiver Operating Characteristic Curve)
The ROC Curve is a graphical representation of the model's performance across different classification thresholds. It plots the True Positive Rate (Recall) against the False Positive Rate (1 - Specificity). A perfect classifier's ROC curve would be a straight line from (0,0) to (1,1), and the area under the curve (AUC) represents the model's overall performance. An AUC close to 1 indicates a good classifier, while an AUC close to 0.5 implies a weak or random classifier.
Conclusion
In Part 1 of this tutorial, we explored the limitations of accuracy in imbalanced datasets and introduced four crucial evaluation metrics: Precision, Recall, F1 Score, and ROC Curve. By adopting these metrics, you can gain deeper insights into your model's performance and make informed decisions on how to handle class imbalance effectively. In Part 2, we will explore various strategies to address the class imbalance problem and improve the model's performance. Stay tuned for the next installment of this series!
Remember, accurately evaluating model performance on imbalanced datasets is the first step towards building robust and unbiased machine learning models.
GitHub Notebook: LINK
YouTube Tutorial: LINK
